Defrag

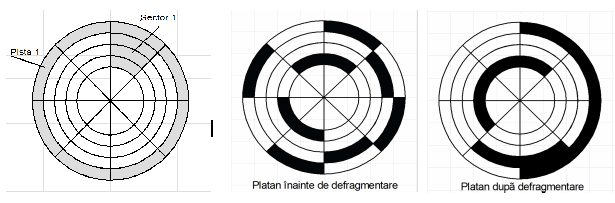
Discul dur (hard disk) este un dispozitiv utilizat pentru stocarea datelor. Stocarea se face pe o suprafață magnetică dispusă pe platane rotunde metalice. Pe un platan, datele sunt organizate în piste și sectoare, iar zona aflată la intersecția dintre o pistă și un sector poartă denumirea de $cluster$.

Un cluster poate avea două stări: liber, dacă nu conține date, sau ocupat, atunci când conține date.

Un platan se numește defragmentat dacă toți clusterii ocupați de pe fiecare pistă sunt așezați în ordine consecutivă. Defragmentarea se realizează prin mutarea unor clusteri ocupați și are rolul de a micșora timpul de acces la date. Mutarea unui cluster reprezintă transferul datelor de la un cluster ocupat către un cluster liber de pe aceeași pistă.

Cerință

Cunoscând numărul de piste $P$ și de sectoare $S$ al unui platan, numărul și poziția clusterilor ocupați, să se scrie un program care determină :

1. numărul de piste care au toți clusterii liberi;

2. numărul minim de mutări de clusteri, pentru fiecare pistă în parte, astfel încât platanul să devină defragmentat.

Date de intrare

Pe prima linie a fişierului de intrare defrag.in se găsește numărul natural $V$ a cărui valoare poate fi doar $1$ sau $2$.

Pe a doua linie a fișierului de intrare se găsesc două numere naturale $P$ și $S$, separate printr-un spaţiu, cu semnificaţia din enunţ.

A treia linie conţine un număr natural $C$ reprezentând numărul total de clusteri ocupați de pe platan, iar pe fiecare din următoarele $C$ linii se găsește câte o pereche de valori $p_i$ şi $s_i$, $1 \leq i \leq C$, separate printr-un spaţiu, reprezentând pista, respectiv sectorul unde se află fiecare cluster ocupat.

Date de ieşire

Fișierul de ieșire este defrag.out.

Dacă valoarea lui $V$ este $1$ atunci fişierul de ieşire va conţine pe prima linie un număr natural ce reprezintă numărul de piste care au toți clusterii liberi.

Dacă valoarea lui $V$ este $2$ atunci fişierul de ieşire va conține pe prima linie $P$ numere naturale notate $M_i$, $1 \leq i \leq P$, separate prin câte un singur spațiu, unde $M_i$ reprezintă numărul minim de mutări de clusteri, dintre cei aflați pe pista $i$, astfel încât pe pista $i$ clusterii ocupați să se găsească într-o ordine consecutivă.

Restricţii şi precizări

• $1 \leq p \leq 100$

• $1 \leq S \leq 360$

• $1 \leq C \leq P*S$

• pistele sunt numerotate de la $1$ la $P$ începând cu pista exterioară

• sectoarele sunt numerotate de la $1$ la $S$ în sensul acelor de ceasornic începând cu sectorul $1$

• dacă o pistă are toți clusterii liberi, atunci valoarea cerută la a doua cerință este $0$

• 20% din teste vor avea valoarea $V = 1$, iar 80% din teste vor avea valoarea $V = 2$.

Exemplul 1

defrag.in

1 
4 8
10
1 1
1 3
1 5
1 7
4 5
4 1
4 6
4 8
2 2
2 4

defrag.out

1

Explicaţii

Datele corespund figurilor anterioare : $V = 1$

• Numărul de piste $P = 4$ , numărul de sectoare $S = 8$

• Numărul total de clusteri ocupați este $C = 10$ (cei marcați cu negru)

• Pe prima pistă sunt $4$ clusteri ocupați, în sectoarele $1$, $3$, $5$ si $7$.

• Pe a doua pistă sunt $2$ clusteri ocupați, în sectoarele $2$ și $4$.

• Pe a treia pistă nu sunt clusteri ocupați.

• Pe a patra pistă sunt $4$ clusteri ocupați, în sectoarele $1$, $5$, $6$ și $8$.

O singură pistă are toți clusterii liberi, pista numărul $3$, deci valoarea cerută este $1$.

Exemplul 2

defrag.in

2 
4 8
10
1 1
1 3
1 5
1 7
4 5
4 1
4 6
4 8
2 2
2 4

defrag.out

2 1 0 1

Explicaţii

Datele corespund figurilor anterioare : $V = 2$

• Pe prima pistă sunt necesare minim două mutări de clusteri pentru ca toți clusterii ocupați să se găsească într-o ordine consecutivă, deci valoarea cerută este $2$.

• Pe a doua pistă este suficientă o singură mutare de cluster, pentru ca toți clusterii ocupați să se găsească într-o ordine consecutivă, deci valoarea cerută este $1$.

• Pe a treia pistă nu sunt clusteri ocupați, deci valoarea cerută este $0$.

• Pe a patra pistă este suficientă o singură mutare de cluster, pentru ca toți clusterii ocupați să se găsească într-o ordine consecutivă, deci valoarea cerută este $1$.