MaxCiun
Legenda Ciunului lui Eratostene
Se zice că prin vara anului 212 Î.H., Valy și Eratostene stăteau, ca de obicei, la o discuție aprinsă despre algoritmi. Aceștia lucrau la un nou algoritm pentru determinarea numerelor prime (mai bine spus, Valy scria algoritmul în timp ce Eratostene se prefăcea că îl ajută). Mândri de creația lor revoluționară, cei doi hotărăsc să numească algoritmul “Ciunul lui Eratostene”, și așa avea să se numească până într-o noapte furtunoasă din anul 207 Î.H.
În acea noapte, cuprins de invidie, Eratostene decide să schimbe numele algoritmului în “Ciurul lui Eratostene”, folosindu-și influența pentru a rescrie istoria. Valy nu s-a lăsat, și a jurat că se va răzbuna. În dorința de a-și face cunoscută contribuția, a decis că în această problemă algoritmul va purta adevăratul lui nume!
Cerință
Mai jos aveți cea mai nouă variantă a algoritmului “Ciunul lui Eratostene”, concepută de Valy chiar ieri. Valy vrea să ruleze acest algoritm pe un procesor care poate executa maxim $T$ iterații pe secundă. Numărul de iterații este dat de valoarea variabilei iters la finalul execuției. Treaba voastră este să găsiți $N$-ul maxim pentru care algoritmul se va executa în cel mult o secundă.
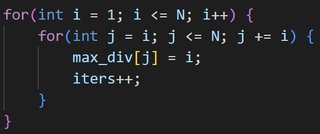
Date de intrare
Pe prima linie se va afla un număr $T$, numărul de iterații pe secundă pe care le suportă procesorul.
Date de ieșire
Pe prima linie se va afișa numărul $N$ cerut.
Subtask-uri
| |
Punctaj | Restricții |
|---|---|---|
| 1 | 27 | $1 \leq T < 7077$ |
| 2 | 39 | $1 \leq T < 13970038$ |
| 3 | 34 | $1 \leq T < 20877697666$ |
Exemple
Intrare
11
Ieșire
5
Explicația exemplului
Pentru $N = 1$, algoritmul face $1$ iterație
Pentru $N = 2$, algoritmul face $3$ iterații
Pentru $N = 3$, algoritmul face $5$ iterații
Pentru $N = 4$, algoritmul face $8$ iterații
Pentru $N = 5$, algoritmul face $10$ iterații
Pentru $N = 6$, algoritmul face $14$ iterații
Deci $N = 5$ este cel mai mare care se încadrează într-o secundă
-
Autor: Bogdan-Ioan Popa Publicat de: Oepeling -
Tags:
Căutare binară sqrt