Valutar

Valutar este un joc care poate fi jucat de oricâți jucători. La începutul jocului, fiecare jucător primește $L$ lei și $E$ euro, precum și un jeton numerotat cu numărul jucătorului. Mai exact, dacă există $M$ jucători, vor fi $M$ jetoane, numerotate de la $1$ la $M$. Tabla de joc este harta unui oraș pe care este ilustrat un traseu circular ce conține $N$ case de schimb valutar, numerotate în ordinea de pe traseu de la $1$ la $N$. Fiind circular, după casa $N$ urmează casa $1$. Pentru fiecare casă de schimb valutar se cunosc două valori $C$ și $V$ ($C$ reprezintă câți lei plătește un jucător dacă vrea să cumpere $1$ euro de la casa respectivă, iar $V$ reprezintă câți lei primește jucătorul dacă vrea să vândă $1$ euro). Fiecare casă are o anumită culoare în funcție de care jucătorul ajuns în punctul respectiv trebuie să efectueze o anumită acțiune astfel:

Inițial toți jucătorii pornesc de la casa de schimb valutar $1$ care este albă. Jucătorii mută pe rând în ordinea jetoanelor. Mai întâi mută jucătorul $1$, apoi $2$, $3$, …, $N$. După jucătorul $N$ va muta din nou $1$ etc. La o mutare, un jucător care nu a fost eliminat din joc:
- “dă” cu zarul electronic; zarul va afișa un număr întreg $nr$;
- avansează cu nr poziții (adică dacă jetonul său este la casa $i$ va ajunge la casa $i + nr$);
- execută acțiunea asociată casei de schimb valutar în care a ajuns, în funcție de culoarea acesteia.
Zarul electronic funcționează astfel: la mutarea cu numărul $j$ este generat numărul $nr_j$ calculat după formula:

$nr_j = ( a * nr_{j-1} + b) % N + 1$,

unde $nr_{j-1}$ este numărul generat la mutarea $j-1$; $a$, $b$ și $nr_0$ sunt trei valori cunoscute, iar % reprezintă restul împărțirii întregi (mod).

Cerință

Scrieți un program care să rezolve următoarele cerințe:
1. determină numărul de jucători existenți în joc după $X$ mutări;
2. determină jucătorul care a rămas în joc și care are cea mai mare sumă de Euro după $X$ mutări.

Date de intrare

Fișierul de intrare valutar.in conține pe prima linie cerința care trebuie să fie rezolvată ($1$ sau $2$). Pe a doua linie se află numerele naturale $a$, $b$ și $nr_0$, cu semnificația din enunț. Pe a treia linie se află numerele naturale $N$ $M$ $L$ $E$ $X$, reprezentând numărul de case de schimb valutar, numărul de jucători, câți lei și câți euro primește fiecare jucător la începutul jocului, respectiv numărul de mutări din joc. Pe următoarele $N$ linii sunt descrise casele de schimb valutar, câte o casă pe o linie, în ordinea de la $1$ la $N$, sub forma $Cod$ $C$ $V$, cu semnificațiile din enunț. Valorile scrise pe aceeași linie sunt separate prin câte un spațiu.

Date de ieșire

Fișierul de ieșire valutar.out va conține o singură linie. Dacă cerința este $1$, linia va conține un număr natural reprezentând numărul de jucători existenți în joc după $X$ mutări. Dacă cerința este $2$, linia va conține numărul jetonului jucătorului rămas în joc și care are cea mai mare sumă de euro după $X$ mutări.

Restricții și precizări

• $1 \leq M, C, V \leq 100$
• $1 \leq a, b, nr_0, N, X \leq 10.000$
• $1 \leq L, E \leq 1.000.000$
• Toate casele de schimb valutar au suficienți lei și euro pentru efectuarea oricărei acțiuni.
• Se garantează că pentru datele de test la cerința $2$ va rămâne în joc după $X$ mutări un singur jucător cu suma maximă de euro.
• Pentru fiecare cerință se acordă 50% din punctajul obținut pe teste.

Exemplul 1

valutar.in

1
3 2 7
5 3 2 3 8
A 1 1
G 5 4
G 6 4
V 6 5
R 2 3

valutar.out

1

Exemplul 2

valutar.in

2
3 2 7
5 3 2 3 8
A 1 1
G 5 4
G 6 4
V 6 5
R 2 3

valutar.out

2

Explicație

Numerele care se obțin când se dă cu zarul se generează astfel: $nr_j = (3 * nr_{j-1} + 2) % 5 + 1$, unde $nr_0 = 7$.
Există în joc $5$ case de schimb valutar și $3$ jucători. Toți jucătorii au inițial $2$ lei și $3$ euro și se află la casa de schimb valutar $1$ care este albă. Se efectuează $8$ mutări astfel:

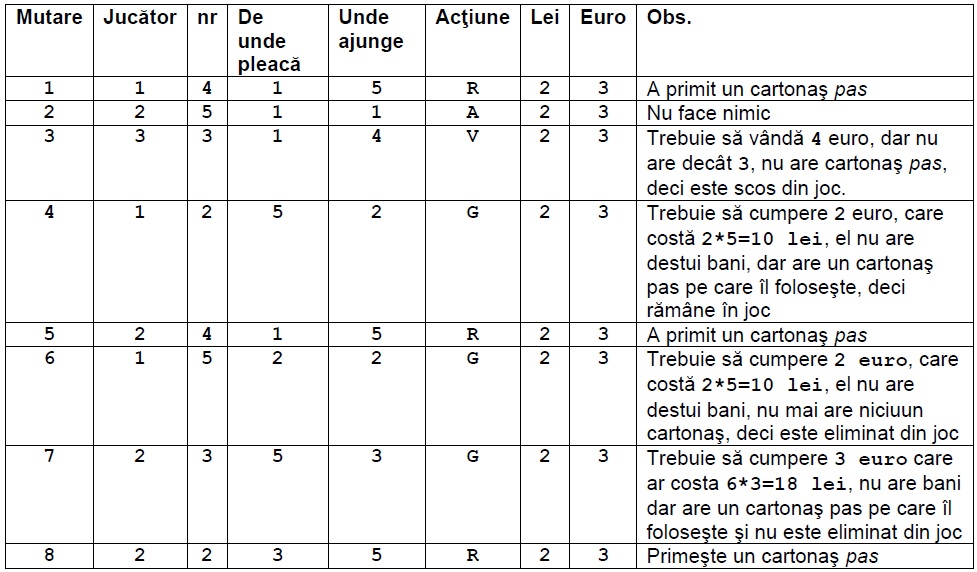
Singurul jucător rămas în joc este $2$, deci el are și suma maximă de euro.